Geometria
Geometria – dziedzina matematyki badająca dla wybranych przekształceń ich niezmienniki, od najprostszych, takich jak odległość, pole powierzchni, miara kąta, przez bardziej zaawansowane, jak krzywizna, punkt stały, czy wymiar. W zależności od rodzaju przekształceń mówi się o różnych rodzajach geometrii.
Geometria, podobnie jak arytmetyka należy do najstarszych nauk. Podobnie jak inne działy matematyki geometria wyewoluowała od badania kształtów znanych z codziennego życia do studiów nad nieskończenie wymiarowymi abstrakcyjnymi przestrzeniami matematycznymi.
*Zadań jest 8 (3 na pierwszym poziomie, 3 na drugim oraz 2 naprawdę trudne) i są uszeregowane poziomami trudności.
*Jeżeli ktoś nie będzie umiał zrobić zadania proszę śmiało pytać (w komentarzach), na pewno w przeciągu paru dni pojawi się odpowiedź, a tych którzy rozwiązali proszę również wrzucać odpowiedzi do komentarzy albo wysyłać na mail, chętnie wprowadzimy ewentualne poprawki. :-)
*Odpowiedzi na obydwa najtrudniejsze zadania są zamieszczone na dole strony, ale najpierw spróbujcie sami je rozwiązać.
POWODZENIA 👍
Poziom 1.
Zadanie 1.
Dany jest trójkąt prostokątny o polu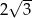 i kącie ostrym
i kącie ostrym 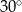 . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Zadanie 2.
Zadanie 1.
Podstawą ostrosłupa jest romb, którego przekątne mają długości 12 i 16. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych rombu w podstawie, a pole powierzchni bocznej jest równe 104. Oblicz objętość ostrosłupa.
Zadanie 2.
Obwód trójkąta prostokątnego wynosi 60 cm, a tangens jednego z kątów ostrych jest równy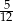 . Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
Zadanie 3.
Poziom 3.
Zadanie 1.
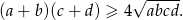
Rozwiązanie 1.
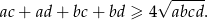
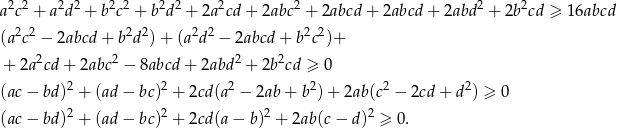
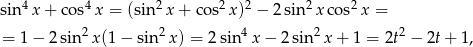
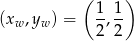
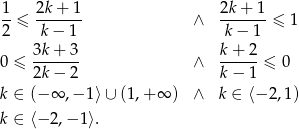
,,Geometria ma dwa wielkie skarby: jednym z nich jest twierdzenie Pitagorasa, a drugim podział odcinka w złoty sposób; pierwszy z nich możemy porównać do złota, a drugi do drogocennego klejnotu." Johannes Kepler
Geometria, podobnie jak arytmetyka należy do najstarszych nauk. Podobnie jak inne działy matematyki geometria wyewoluowała od badania kształtów znanych z codziennego życia do studiów nad nieskończenie wymiarowymi abstrakcyjnymi przestrzeniami matematycznymi.
Tablice geometryczne z encyklopedii z 1728 roku
*Zadań jest 8 (3 na pierwszym poziomie, 3 na drugim oraz 2 naprawdę trudne) i są uszeregowane poziomami trudności.
*Jeżeli ktoś nie będzie umiał zrobić zadania proszę śmiało pytać (w komentarzach), na pewno w przeciągu paru dni pojawi się odpowiedź, a tych którzy rozwiązali proszę również wrzucać odpowiedzi do komentarzy albo wysyłać na mail, chętnie wprowadzimy ewentualne poprawki. :-)
*Odpowiedzi na obydwa najtrudniejsze zadania są zamieszczone na dole strony, ale najpierw spróbujcie sami je rozwiązać.
POWODZENIA 👍
Poziom 1.
Zadanie 1.
Dany jest trójkąt prostokątny o polu
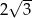 i kącie ostrym
i kącie ostrym 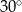 . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta. Zadanie 2.
Liczby 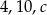 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
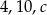 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Zadanie 3.
Dany jest ostrosłup prawidłowy czworokątny o krawędzi bocznej dwa razy dłuższej od krawędzi podstawy.
- Wyznacz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa.
- Wyznacz długość krawędzi ostrosłupa, tak aby pole jego powierzchni bocznej wynosiło
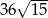
Zadanie 1.
Podstawą ostrosłupa jest romb, którego przekątne mają długości 12 i 16. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych rombu w podstawie, a pole powierzchni bocznej jest równe 104. Oblicz objętość ostrosłupa.
Zadanie 2.
Obwód trójkąta prostokątnego wynosi 60 cm, a tangens jednego z kątów ostrych jest równy
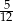 . Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną. Zadanie 3.
Po wydłużeniu każdej krawędzi sześcianu o 2, długość
jego przekątnej podwoiła się. Oblicz pole powierzchni całkowitej
powiększonego sześcianu.
Poziom 3.
Zadanie 1.
Uzasadnij, że jeżeli 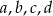 są liczbami dodatnimi to
są liczbami dodatnimi to
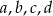 są liczbami dodatnimi to
są liczbami dodatnimi to 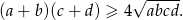
Zadanie 2.
Dla jakich wartości parametru 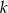 równanie
równanie 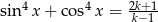 ma rozwiązanie?
ma rozwiązanie?
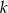 równanie
równanie 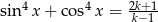 ma rozwiązanie?
ma rozwiązanie? Rozwiązanie 1.
Wymnażając nawiasy z lewej strony nierówności mamy
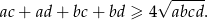
Podnosimy teraz nierówność stronami do kwadratu.
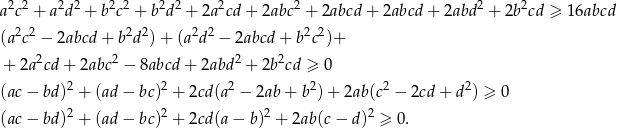
Otrzymana nierówność jest oczywiście spełniona, a przekształcaliśmy w
sposób równoważny, więc wyjściowa nierówność też musi być prawdziwa.
Rozwiązanie 2.
Ze względu na ułamek z prawej strony równości musimy założyć, że 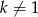 .
.
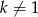 .
.
Przekształćmy lewą stronę równania
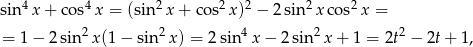
gdzie podstawiliśmy 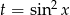 . Spróbujmy ustalić jakie wartości przyjmuje parabola
. Spróbujmy ustalić jakie wartości przyjmuje parabola 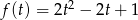 na przedziale
na przedziale 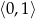 (tak zmienia się
(tak zmienia się 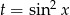 ). Ponieważ jej wierzchołek znajduje się w punkcie
). Ponieważ jej wierzchołek znajduje się w punkcie
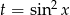 . Spróbujmy ustalić jakie wartości przyjmuje parabola
. Spróbujmy ustalić jakie wartości przyjmuje parabola 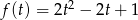 na przedziale
na przedziale 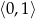 (tak zmienia się
(tak zmienia się 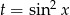 ). Ponieważ jej wierzchołek znajduje się w punkcie
). Ponieważ jej wierzchołek znajduje się w punkcie 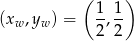
oraz 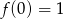 i
i 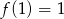 , możliwe wartości
, możliwe wartości 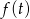 to przedział
to przedział 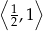 . Podane równanie będzie więc miało rozwiązanie wtedy i tylko wtedy gdy prawa strona równania będzie zawarta w tym przedziale.
. Podane równanie będzie więc miało rozwiązanie wtedy i tylko wtedy gdy prawa strona równania będzie zawarta w tym przedziale.
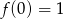 i
i 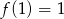 , możliwe wartości
, możliwe wartości 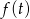 to przedział
to przedział 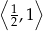 . Podane równanie będzie więc miało rozwiązanie wtedy i tylko wtedy gdy prawa strona równania będzie zawarta w tym przedziale.
. Podane równanie będzie więc miało rozwiązanie wtedy i tylko wtedy gdy prawa strona równania będzie zawarta w tym przedziale. 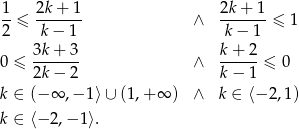



Comments
Post a Comment