Rachunek prawdopodobieństwa

Rachunek prawdopodobieństwa pomaga obliczyć szansę zaistnienia pewnego określonego zdarzenia.

Rachunek prawdopodobieństwa bazuje na kombinatoryce.

Żeby obliczyć szansę dowolnego zdarzenia (nazwijmy go literą A), musimy określić liczbę zdarzeń sprzyjających oraz liczbę wszystkich możliwych zdarzeń (do tego celu stosujemy kombinatorykę). Następnie do obliczenia prawdopodobieństwa korzystamy z jednego wzoru:

P(A)=|A||Ω|

gdzie:
|A| - to liczba zdarzeń sprzyjających (czyli takich, o które nam chodzi) - moc zbioru |A|
|Ω| - to liczba wszystkich możliwych zdarzeń - moc zbioru |Ω|

Pojęcia stosowane w rachunku prawdopodobieństwa:

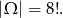
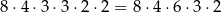
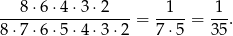
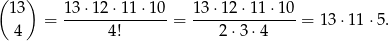
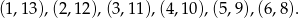
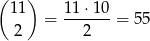
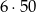
• Doświadczenie losowe - czynność którą wykonujemy, np.: rzut kostką, wybór dnia tygodnia.
• Zdarzenie elementarne - zdarzenie jakie może wydarzyć się w doświadczeniu losowym, np.: wypadło 5                         oczek, wybrano środę.
• Zdarzenie losowe - zbiór jednego lub kilku zdarzeń elementarnych, np.: wypadła parzysta liczba oczek (2, 4, lub 6), wybrano dzień powszedni.
• Moc zbioru - liczba elementów danego zbioru, np.: |{2,4,6}|=3, |{dni powszednie}|=5.

Stosowane oznaczenia:

• Ω - zbiór wszystkich zdarzeń elementarnych doświadczenia losowego, np.: dla rzutu kostką Ω={1,2,3,4,5,6}.
• A - zdarzenie losowe (podzbiór Ω), np.: jeżeli A to zdarzenie polegające na tym, że wypadła parzysta liczba oczek, to: A={2,4,6}.

Mając opanowaną tę wiedzę, możecie śmiało próbować zrobić poniższe zadania.

*Zadań jest 8 (3 na pierwszym poziomie, 3 na drugim oraz 2 naprawdę trudne) i są uszeregowane poziomami trudności.

*Jeżeli  ktoś nie będzie umiał zrobić zadania proszę śmiało pytać (w komentarzach), na pewno w przeciągu paru dni pojawi się odpowiedź, a tych którzy rozwiązali proszę również wrzucać odpowiedzi do komentarzy albo wysyłać na mail, chętnie wprowadzimy ewentualne poprawki.  :-)

*Odpowiedzi na obydwa najtrudniejsze zadania są zamieszczone na dole strony, ale najpierw spróbujcie sami je rozwiązać.

POWODZENIA 👍 

Poziom 1 

Zadanie 1. 

W pudełku jest 15 kul, z czego 3 stanowią kule białe. Jaka jest szansa, że losując kulę trafimy na kulę białą? Wynik podaj w postaci ułamka nieskracalnego.

Zadanie 2.

W magazynie jest 7 misiów, 8 lalek, 10 samochodzików i 5 robotów. Jakie jest prawdopodobieństwo, że losując jedną rzecz z magazynu 

Zadanie 3.

W pewnym miejscu na świecie każdego dnia szansa na deszcz wynosi 1/3. Jakie jest prawdopodobieństwo, że przez trzy dni z rzędu NIE będzie tam padać deszcz?

Poziom 2

Zadanie 1.

Rzucamy trzy razy monetą, a następnie rzucamy tyle razy kostką, ile orłów otrzymaliśmy w rzutach monetami. Oblicz prawdopodobieństwo tego, że suma oczek otrzymanych w rzutach kostką jest dwa razy większa od liczby orłów otrzymanych w rzutach monetą jeżeli wiadomo, że w rzutach monetą otrzymaliśmy przynajmniej jednego orła.

Zadanie 2.

Z pojemnika, w którym są dwa losy wygrywające i trzy losy puste, losujemy dwa razy po jednym losie bez zwracania. Oblicz prawdopodobieństwo, że otrzymamy co najmniej jeden los wygrywający. Wynik przedstaw w postaci ułamka nieskracalnego.

Zadanie 3.

Spośród liczb naturalnych trzycyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby, która przy dzieleniu przez 11 daje resztę 3.

Poziom 3

Zadanie 1

Liczby 1, 2, 3, 4, 5, 6, 7, 8 ustawiamy losowo w szeregu. Oblicz prawdopodobieństwo, że w tym ustawieniu suma każdych dwóch sąsiednich liczb będzie nieparzysta. Wynik podaj w postaci ułamka nieskracalnego.

Zadanie 2 

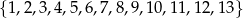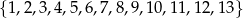Ze zbioru liczb  losujemy bez zwracania 4 liczby. Oblicz jakie jest prawdopodobieństwo, że wśród 4 otrzymanych liczb jest dokładnie jedna para liczb o sumie równej 14.

 UWAGA ROZWIĄZANIA!!!

Rozwiązanie 1

Wszystkich możliwych ustawień 8 liczb jest

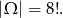
W zdarzeniach sprzyjających na przemian muszą stać liczby parzyste i liczby nieparzyste.

Policzmy takie zdarzenia. Pierwszą liczbę wybieramy dowolnie – na 8 możliwych sposobów. Drugą możemy już wybrać tylko na 4 sposoby, bo musi mieć inną parzystość niż pierwsza. Trzecią możemy wybrać na 3 sposoby – musi tej samej parzystości co pierwsza i musi być od niej różna. Czwartą możemy wybrać też 3 sposoby – musi mieć taką samą parzystość jak druga i być od niej różna. Analogicznie piątą i szóstą liczbę możemy wybrać na 2 sposoby, a przy wyborze liczb siódmej i ósmej nie mamy już żadnego wyboru. Zatem jest

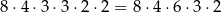
zdarzeń sprzyjających i prawdopodobieństwo wynosi

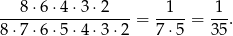
Rozwiązanie 2 

Wszystkich zdarzeń elementarnych jest

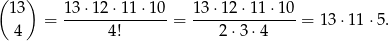
Wypiszmy wszystkie pary liczb, które w sumie dają 14.

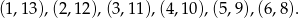
Jest jeszcze liczba 7, która nie ma pary (bo losujemy bez zwracania).

Sposób I

O zdarzeniach sprzyjających myślimy następująco: musimy wybrać jedną z powyższych par, a potem musimy dobrać jeszcze dwie liczby tak, aby nie były z jednej pary.

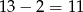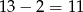Jedną parę możemy wybrać na 6 sposobów. Po wybraniu tej pary pozostaje  liczb i z nich musimy wybrać jeszcze dwie. Dwie pozostałe liczby możemy wybrać na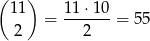

sposobów. Od tych 55 możliwych par musimy jednak odjąć 5 par, w których suma jest równa 14. W sumie 3 i 4 liczbę możemy więc wybrać na 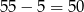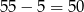 sposobów. Jest więc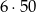

zdarzeń sprzyjających i prawdopodobieństwo jest równe